Normalization explained
Understand how to normalize your data

What is normalization?1
You’ve identified your big why, its indicators, and the datasets that support those indicators. Now you’re looking at a data table (or tables) full of mismatched units of measure. This isn’t a problem. A big why has many facets and can be measured in more than one way– that’s exactly what a compiled indicator does.
In this section, we will talk about math and some formulas. This is important because we want to be able to compare apples to apples. To be able to do this, we need all the data points to be in the
same unit of measure. We’ll break this down step-by-step for you.
The process of converting data points to a common unit is called normalization. There are many ways to normalize your data, and the min-max normalization method works well for our purposes to create a compiled indicator.
Here’s how it works:
- First, the minimum value equals 0
- Next, the maximum value equals 1
- Finally, every other value in between becomes a decimal value.
Let’s walk through an example below.
Set the stage
Imagine that your big why is public engagement. Two indicators of public engagement are visitor satisfaction and number of visitors. You have data points for these indicators: several years of survey satisfaction scores and visitor counts. The datasets look like this.
Sample survey satisfaction scores
The table below is a small sample from thousands of survey responses you’ve received over the last five years. Each row in the chart represents an individual response from a single person, labeled with the year it was submitted. It shows that two individuals responded in 2023, 2021, and 2020, and one individual responded in 2022 and 2019. (In real life, this chart would be thousands of lines long, we’re just pretending for the sake of simplicity that the survey only got one or two responses per year.)
| Survey Year | Satisfaction (1-5, where 1=Very unsatisfied and 5=Very satisfied) |
|---|---|
| 2023 | 5 |
| 2023 | 2 |
| 2022 | 3 |
| 2021 | 4 |
| 2021 | 1 |
| 2020 | 5 |
| 2020 | 3 |
| 2019 | 4 |
Visitor counts
The table below is a count of the visitors to an exhibition over the last five years.
| Year | Visitors |
|---|---|
| 2023 | 2,602,981 |
| 2022 | 2,047,293 |
| 2021 | 1,109,098 |
| 2020 | 1,578,391 |
| 2019 | 3,495,209 |
It doesn’t make sense to squish together a five-point survey score and a quantity of people, so we’ll need to normalize our data. Here is what the min-max normalization formula means.
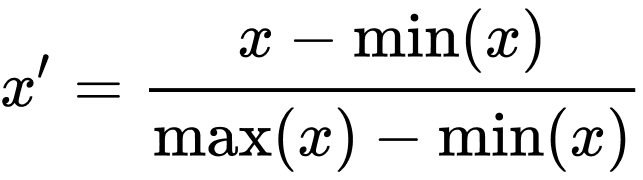
- x is the number you’re normalizing
- min(x) is the smallest number in the data series
- max(x) is the largest number
- x-min(x) is the difference between the number to be normalized and the smallest number
- max(x)-min(x) is the difference between the largest number and the smallest number
- x’ is the new, normalized value of x.
As you may remember from high school math, subtract the bits on the top and bottom of the fraction first, and then divide. The normalized value of x equals (x-min(x)) divided by (max(x)-min(x)).
To check your work, make sure that x’ isn’t less than 0 or greater than 1.
Gather materials
You’ll need access to spreadsheet software, but you can also do this manually.
To normalize the survey satisfaction scores, start by finding the largest and smallest numbers in the column:
| Survey Year | Satisfaction (1-5, where 1=Very unsatisfied and 5=Very satisfied) |
|---|---|
| 2023 | 5 Maximum |
| 2023 | 2 |
| 2022 | 3 |
| 2021 | 4 |
| 2021 | 1 Minimum |
| 2020 | 5 Maximum |
| 2020 | 3 |
| 2019 | 4 |
In the satisfaction score column above, the year 2021 stands as the minimum (1), and both 2023 and 2020 are the maximum (5), thus we can write min(x)=1 and max(x)=5
Next, we’ll need to “normalize” all the numbers that are in-between the min and max. In this example, that means we need to normalize 2, 3, and 4. Let’s start by normalizing the score of 2 from 2023.
To begin, we say that x=2. The formula is:
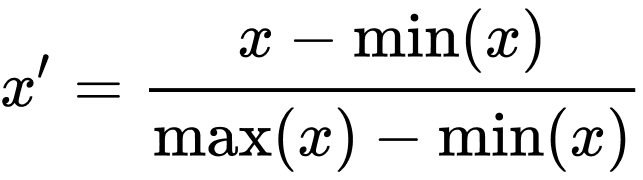
When you substitute 2 for x, 1 for min(x), and 5 for max(x), the normalized value of x equals 1/4.
-
Subtract first: 2 - 1 = 1, and 5 - 1 = 4 or 1/4.
-
1/4 = 0.25, so normalization rescales the score of 2 to 0.25
Check your work: 0.25 isn’t less than 0 or greater than 1, so it’s a valid normalized data point. You can apply the same calculation to all the other scores in the table:
| Survey Year | Satisfaction | Min Max Method | Normalized Satisfaction Score (x’) |
|---|---|---|---|
| 2023 | 5 | 5-1/5-1 | 1 |
| 2023 | 2 | 2-1/5-1 | .25 |
| 2022 | 3 | 3-1/5-1 | .5 |
| 2021 | 4 | 4-1/5-1 | .75 |
| 2021 | 1 | 1-1/5-1 | 0 |
| 2020 | 5 | 5-1/5-1 | 1 |
| 2020 | 3 | 3-1/5-1 | .5 |
| 2019 | 4 | 4-1/5-1 | .75 |
This is a very small example, and real survey datasets can contain thousands of rows. Instead of normalizing every score by hand, you can write a formula in Excel or Google Sheets.
In a spreadsheet, use the formula =(B2-min(B:B))/(max(B:B)-min(B:B))
- B2 contains the score that you want to normalize.
- B:B is the column containing the whole data series, so min(B:B) will select min(x), and max(B:B) will select max(x).
- If the data series to be normalized is not located in column B, substitute the actual locations of the data in place of B:B and B2.
Copy the formula to all the rows in the dataset. You’ve successfully normalized the survey dataset.
Now, do the same for the “visitor count” dataset. Assuming that your data is in column C, do that quickly with this spreadsheet formula: =(C2-min(C:C))/(max(C:C)-min(C:C))
Copy the formula to the other rows:
Now the visitor count and the satisfaction scores are both on a scale between 0 and 1. You can combine the two indicators mathematically without the mismatched units of measure getting in the way.
Since the visitor data is reported by year, calculate the average satisfaction score for each year using the normalized values.
Tool tip: The AVERAGEIF function finds all the rows where column I=B2 (the two year columns match) and then averages those rows’ values from column K (normalized satisfaction score). AVERAGEIF works in both Excel and Google Sheets, and it’s a useful tool when you need to aggregate data by year, state, agency, etc.
Finally, calculate the composite indicator for public engagement by averaging the normalized visitors and average survey score (normalized) for each year.
You have successfully turned two mismatched datasets into a single composite indicator representing multiple facets of your big why.
Footnotes
-
This section was authored by Katherine Petway with Ana Monroe serving as editor. ↩
